101.

Pravougaonik konstruisan na racionalnoj duži i jednak kvadratu na "duži koja sa racionalnom obrazuje celo medijalno" ima za širinu petu apotomu.

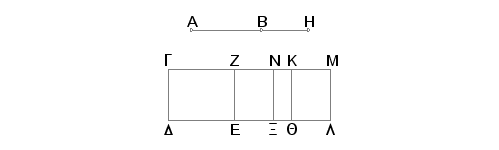
Neka je AB "duž koja sa racionalnom obrazuje celo medijalno", GD racionalna duž i na GD je konstruisan pravougaonik GE, jednak kvadratu na AB, sa širinom GZ. Tvrdim da je GZ peta apotoma.
Zaista, neka je BH dodatak za AB. Tada su AH i HB duži nesamerljive u stepenu, zbir kvadrata na njima medijalan, a dvostruki pravougaonik obrazovan od njih raciomalan. I konstruišimo na GD pravougaonik GQ, jednak kvadratu na AH, i pravougaonik KL, jednak kvadratu na HB. Prema tome je cela površina GL jednaka zbiru kvadrata na AH i na HB. No zbir kvadrata na AH i na HB je medijalan, te je medijalna i površina GL. A ona je konstruisana na racionalnoj duži GD i ima širinu GM, zbog toga je racionalna i duž GM i nesamerljiva sa GD. I pošto je cela površina na GL jednaka zbiru kvadrata na AH i na HB, a površina GE jednaka kvadratu na AB, biće ostatak ZL jednak dvostrukom pravougaoniku sa stranama AH i HB. Prepolovimo ZM tačkom N i povucimo kroz N pravu NX paralelnu svakoj od GD i ML. Tada je svaka od površina ZX, NL jednaka pravougaoniku sa stranama AH i HB. I pošto je dvostruki pravougaonik sa stranama AH, HB racionalan i jednak površini ZL, racionalna je i površina ZL. I konstruisana je na racionalnoj duži EZ i ima širinu ZM. Prema tome je racionalna i duž ZM i samerljiva po dužini sa GD. A kako je GL medijalno, a ZL racionalno, biće GL nesamerljivo sa ZL. No GL je prema ZL kao GM prema MZ, prema tome je duž GM nesamerljiva po dužini sa MZ. I obe su one racionalne. Znači GM i MZ su racionalne, samerljive samo u stepenu. Na ovaj način GZ je apotoma.
Tvrdim da je peta.
Zaista, slično se dokazuje da je pravougaonik sa stranama GK i KM jednak kvadratu na NM, tj. četvrtini kvadrata na ZM. I pošto je kvadrat na AH nesamerljiv sa kvadratom na HB, kvadrat na AH jednak jednak površini GQ, kvadrat na HB površini KL, biće i površina GQ nesamerljiva sa površinom KL. A kako je GQ prema KL kao GK prema KM, biće nesamerljiva po dužini i duž GK sa duži KM. Pošto su sada GM i MZ dve nejednake duži i na GM je konstruisan pravougaonik jednak četvrtini kvadrata na ZM, sa kvadratnom dopunom, a on deli GM na nesamerljive delove, biće kvadrat na GM veći od kvadrata na MZ za kvadrat na duži nesamerljivoj se GM. I dodatak ZM je nesamerljiv sa datom racionalnom duži GD. Na ovaj način je GZ peta apotoma. A to je trebalo dokazati.