110.

Pri oduzimanju od jedne medijalne površine druge medijalne površine, nesamerljive sa prvom, pojavljuju se dve ostale iracionale druga medijalna apotoma ili duž koja sa medijalnom obrazuje celo medijalno.

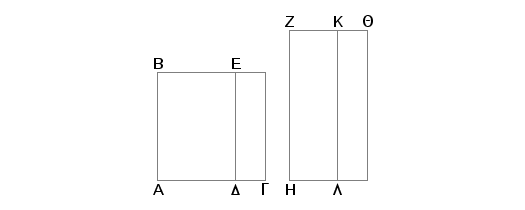
Oduzmimo, slično kao na prethodnim slikama, od medijalne površine BG medijalnu površinu BD nesamerljivu sa celom. Tvrdim, da se kao strana kvadrata jednakog površini EG pojavljuje jedna od dve iracionale, ili druga medijalna apotoma ili duž koja sa medijalnom obrazuje celo medijalno.
Zaista, pošto je svaka od površina BG i BD medijalna i BG je nesamerljivo sa BD, biće svaka od ZQ i ZK racionalna i nesamerljiva po dužini sa ZH. I pošto je BG nesamerljivo sa BD, tj. HQ sa HK, biće i QZ nesamerljivo sa ZK. Prema tome su duži ZQ i ZK racionalne i samerljive samo u stepenu. Znači, KQ je apotoma (a ZK je dodatak. I kvadrat na ZQ je veći od kvadrata na ZK za kvadrat na duži, koja je ili samerljiva sa ZQ ili nesamerljiva).
Ako je kvadrat na ZQ veći od kvadrata na ZK za kvadrat na duži samerljivoj sa ZQ, i nijedna od ZQ i ZK nije samerljiva po dužini sa datom duži ZH, biće KQ treća potoma. No KL je racionalan duž, a pravougaonik obuhvaćen racionalnom duži i trećom apotomom je iracionalan, i strana jednakog mu kvadrata takođe je iracionalna i zove se druga medijalna apotoma. Prema tome je strana kvadrata jednakog površini LQ, tj, površini EG, jednaka drugoj medijalnoj apotomi.
A ako je kvadrat na ZQ veći od kvadrata na ZK za kvadrat na duži nesamerljivoj po dužini sa ZQ, i nijedna od duži QZ i ZK nije samerljiva po dužini sa ZH, KQ je šesta apotoma. No strana kvadrata, jednakog pravougaoniku obuhvaćenom racionalnom duži i šestom apotomom, jednaka je "duži koja sa medijalnom obrazuje celo medijalno". Na ovaj način, strana kvadrata jednakog površini LQ, tj. površini EG, jednaka je "duži koja sa medijalnom obrazuje celo medijalno". A to je trebalo dokazati.