43.
Prva bimedijala se deli samo jednom tačkom.
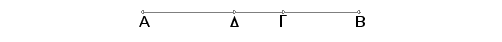
Neka je AB prva medijala, podeljena tačkom G tako da AG i GB budu medijale samerljive samo u stepenu i da obuhvataju racionalni pravougaonik. Tvrdim da se AB ne deli drugom tačkom.
Zaista, ako je to moguće, neka se deli i tačkom D i to takoda su AD i DB medijale samerljive samo u stepenu i obuhvataju racionalan pravougaonik.
Pošto se sad, onim čime se razlikuje dvostruki pravougaonik sa stranama AD i DB od dvostrukog pravougaonika sa stranama AG i GB, time razlikuje i zbir kvadrata na AD i na DB, dok se dvostruki pravougaonik sa AD i DB razlikuje od dvostrukog pravougaonika na stranama AG i GB za racionalnu veličinu, jer su oba racionalna. Prema tome se razlikuje za racionalnu veličinu i zbir kvadrata na AG i na GB od zbira kvadrata na AD i na DB, a oni su oba medijalni. A to je besmisleno.
Na ovaj način prva bimedijala se ne deli i jednom i drugom tačkom na svoje delove. Prema tome ona se deli samo jednom tačkom. A to je trebalo dokazati.