47.
"Strana kvadrata jednakog zbiru dve medijalne površine" deli se samo jednom tačkom.
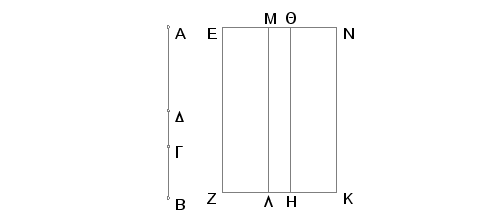
Neka je AB "strana kvadrata jednakog zbiru dve medijalne površine", koja se deli tačkom G tako da su AG i GB nesamerljive u stepenu i da je zbir kvadrata na AG i na GB medijalan i pravougaonik sa stranama AG i GB medijalan i nesamerljiv sa zbirom kvadrataa na njima. Tvrdim da se AB ne deli drugom tačkom pod navedenim uslovima.
Zaista, ako je to moguće, neka se deli i tačkom D i to tako, razume se, da duž AG ne bude jednaka sa DB, već predpostavljamo da AG bude veća. Uzmimo racionalnu duž EZ i konstruišimo na EZ pravougaonik EH jednak zbiru kvadrata na AG i na GB. Tada je ceo pravougaonik EK jednak kvadratu na AB. Zatim konstruišimo na EZ pravougaonik ED jednak zbiru kvadrata na AD i na DB. Tada je dvostruki pravougaonik sa stranama AD i DB, kao ostatak, jedan ostatku,pravougaoniku MK. I pošto se pretpostavlja da je zbir kvadrata na AG i na GB medijalan, biće medijalan i pravougaonik EH. A on je konstruisan na racionalnoj duži EZ. Biće prema tome racionalna i duž QE i nesamerljiva po dužini sa EZ. Iz istih razloga je racionalna i duž QN i nesmerljiva po dužini sa EZ. I pošto je zbir kvadrata na AG i na GB nesamerljiv sa dvostrukim pravougaonikom kome su strane AG i GB, biće i pravougaonik kome su strane AG i GB, biće i pravougaonik EH nesamerljiv sa pravougaonikom HN. Pa prema tome je i duž EQ nesamerljiva sa duži QN. A one su racionalne. Na ovaj način su duži EQ i QN racionalne i samerljive samo u stepenu. Znači EN je binomijala, koja se deli tačkom Q. Na sličan način se dokazuje da se ona deli i tačkom M. A pri tome EQ nije isto što i MN. Na ovaj način se binomijala deli i jednom i drugom tačkom. A to je besmisleno. Prema tome se "strana kvadrata jednakog zbiru dve medijalne površine" ne deli i jednom i drugom tačkom. Na ovaj način ona se deli samo jednom tačkom.