55.

Ako su racionalna duž i druga binomijala strane nekog pravougaonika, biće strana kvadrata sa površinom jednakom tom pravougaoniku iracionalna i to prva bimedijala.

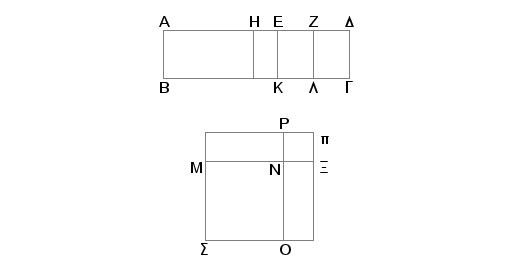
Neka je površina ABGD obuhvaćena racionalnom duži AB i drugom binomijalom AD. Tvrdim, da je strana kvadrata sa površinom jednakom ABGD prva bimedijala.
Pošto je AD druga binomijala, podelimo je tačkom E na delove i neka veći deo bude AE. Na ovaj način su duži AE i ED racionalne i samerljive samo u stepenu i kvadrat na AE veći od kvadrata na ED za kvadrat na duži koja je samerljiva sa AE i da je manji deo ED samerljivo po dužini sa AB. Prepolovimo ED tačkom Z i konstruišimo na AE pravougaonik, sa vkadratnom dopunom, jednak kvadratu na EZ sa stranama AH i HE. Biće tada AH samerljivo po dužini sa HE. I povucimo iz tačka H, E, Z prave HQ, EK ZL paralelne sa AB i GD. Dalje, konstruišimo kvadrat SN jednak pravougaoniku AQ i kvadrat Np jednak pravougaoniku HK i to tako da strane MN i NX budu na istoj pravoj. Tada će na istoj pravoj biti i strane PN i NO. I dopunimo kvadrat Xp. Jasno je iz ranije dokazanog da je MP srednja proporcionala za SN i Np i da je jednaka površini EL i da je AG jednako površini kvadrata na MX. Treba dokazati da je MX prva bimedijala. Pošto je AE nesamerljivo po dužini sa ED, a ED samerljivo sa AB, biće AE nesamerljivo sa AB. I pošto je AH samerljivo sa AB, biće i AE samerljivo sa svakim od AH i HE. No AE je nesamerljivo po dužini sa AB. Prema tome su AH i HE nesamerljive sa AB. Na ovaj način su BA, AH, HE racionalne samerljive samo u stepenu. Zbog toga je svaka od površina AQ i HK medijalna, a prema tome i svaki od kvadrata je medijalan, a njihove strane MN i NX medijalne. I pošto je AH samerljivo po dužini sa HE, samerljivo je i AQ sa HK, tj. SN sa Np tj. kvadrat na MN sa kvadratom na NX [pa prema tome je MN samerljivo sa NX u stepenu]. I pošto je AE nesamerljivo po dužini sa ED, a AE je samerljivo sa AH, i ED samerljivo sa EZ, biće AH nesamerljivo sa EZ. A prema tome i AQ nesamerljivo sa EL, tj. SN sa MP, tj. ON sa NP, tj. MN nesamerljivo po dužini sa NX. A dokazali smo da su MN i NX i medijale i samerljive u stepenu. Na ovaj način su MN i NX medijale samerljive samo u stepenu. Tvrdim da one obuhvataju racionalnu površinu. Zaista, pošto se pretpostavlja da je DE samerljivo sa svakom od AB i EZ, biće samerljiva i EZ sa EK. I svaka od njih je racionalan. Na ovaj način je racionalna i površina EL, tj. MP. Ali MP je površina sa stranama MN i NX. A ako se saberu dva medijala, samerljive samo u stepenu, koje obuhvataju racionalnu površinu, biće i cela duž iracionalna i to prva bimedijala.
Na ovaj način je MX prva bimedijala.