84.
Duži koja se medijalnom obrazuje celo medijalno se može dodati jedna jedina duž, u stepenu nesamerljiva sa celom, koja zajedno sa celom obrazuje zbir kvadrata na tim dužima medijalan, obuhvata sa njom medijalan dvostruki pravougaonik i pri tome je pomenuti zbir kvadrata nesamerljiv sa tim dvostrukim pravougaonikom.
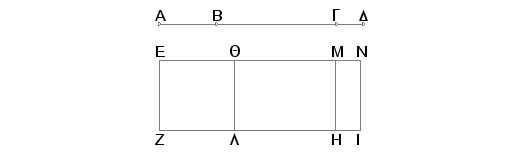
Neka je AB "duž koja sa medijalnom obrazuje celo medijalno", a BG duž koja joj se dodaje. Znači AG i GB su duži, nesamerljive u stepenu, koje obrazuju traženo. Tvrdim, da se ne može dodati duži AB nikakva druga duž koja zadovoljava iste uslove.
Zaista, ako može, dodajmo BD. Na taj način su i duži AD i DB nesmaerljive u stepenu, zbir kvadrata na AD i na DB je medijalan, dvostruki pravougaonik sa stranama AD i DB je takođe medijalan i zbir kvadrata na AD i na DB je nesamerljiv sa dvostrukim pravougaonikom sa stranama AD i DB. Odmerimo racionalnu duž EZ i konstruišimo na EZ pravougaonik EH, širine EM, jednak zbiru kvadrata na AG i na GB, a zatim i na duži EZ konstruišimo pravougaonik QH, širine QM, jednak dvostrukom pravougaoniku kome su strane AG i GB. Tada je ostatak, kvadrat na AB, jednak pravougaoniku EL. Prema tome je AB strana kvadrata jednakog pravougaoniku EL. Zatim, konstruišimo na EZ pravougaonik EI, širine EN, jednak zbiru kvadrata na AD i na DB. Tada je kvadrat na AB jednak površini EL. Znači ostatak, dvostruki pravougaonik sa stranama AD i DB, jednak je pravougaoniku QI. I kako je zbir kvadrata, na AG i na GB medijalan i jednak površini EH, biće i ta površina EH medijalna. A kako je ona konstruisana na racionalnoj duži EZ i ima širinu EM, biće i EM racionalna i nesamerljiva po dužni sa EZ. Zatim, pošto je dvostruki pravougaonik kome su strane AG i GB medijalan i jednak površini QH, biće medijalna i ta površina QH. A pošto je konstruisana na racionalnoj duži EZ i ima širinu QM, biće i QM racionalna duž i nesamerljiva po dužini sa EZ. I pošto je zbir kvadrata na AG i na GB nesamerljiv sa dvostrukim pravougaonikom kome su strane AG i GB, nesamerljiva je i površina EH sa površinom QH. Tada je duž EM nesamerljiva po dužini sa MQ. A obe su racionalne. Znači EM i MQ su racionalne, samerljive samo u stepenu. Prema tome EQ je apotoma i QM je njoj dodata duž. Slično se dokazuje da je i EQ apotoma, a njoj dodata duž QN. Na ovaj način apotomi se može dodati i jedna i druga duž, svaka samerljiva samo u stepenu sa celom, a to je, na sonovu dokazanog nemoguće. Prema tome se duži AB ne može dodati nikakva druga duž.
Na ovaj način, "duži koja sa medijalnom obrazuje celo medijalno" se može dodati jedna jedina duž, u stepenu nesamerljiva sa celom, koja sa celom obrazuje zbir kvadrat na tim dužima medijalan, obuhvata sa njom medijalan dvostruki pravougaonik i pri tome je pomenuti zbir kvadrata nesamerljiv sa tim dvostrukim pravougaonikom. A to je trebalo dokazati.