Krugovi se odnose jedan prema drugom kao kvadrati na prečnicima.

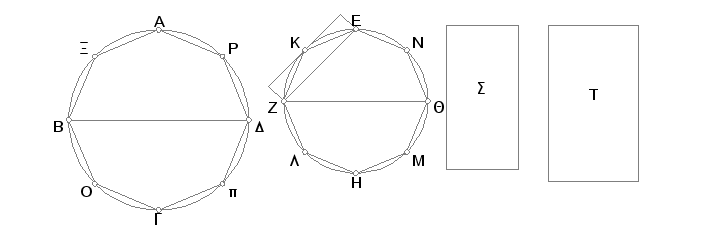
Neka su ABGD i EZHQ krugovi, a BD i ZQ njihovi prečnici. Tvrdim da se krug ABGD odnosi prema krugu EZHQ kao kvadrat na BD prema kvadratu na ZQ.
Zaista, ako se krug ABGD ne odnosi prema krugu EZHQ kao kvadrat na BD prema kvadratu na ZQ, biće razmera kvadrata na BD prema kvadratu na ZQ jednaka razmeri kruga ABGD prema površini ili manjoj ili većoj od površine kruga EZHQ. Neka bude, prvo, prema manjoj S. Upišimo u krug EZHQ kvadrat EZHQ. Taj upisani kvadrat je veći od polovine kruga EZHQ. Jer, ako kroz tačke E, Z, H, Q povučemo tangente na krug, polovina opisanog kvadrata jednaka je kvadratu EZHQ; a kako je opisani kvadrat veći od kruga, biće upisani kvadrat EZHQ veći od polovine kruga EZHQ. Prepolovimo lukove EZ, ZH, HQ, QE tačkama K, L, M, N i povucimo duži EK, KZ, ZL, LH, HM, MQ, QN i NE; tada je svaki od trouglova EKZ, ZLH, HMQ, QNE veći od polovine odgovarajućeg kružnog segmenta. Jer, ako kroz tačke K, L, M, N povučemo tangente na krug i na pravima EZ, ZH, HQ, QE konstruišemo paralelograme, svaki od trouglova EKZ, ZLH, HMQ, QNE jednak je polovini odgovarajućeg paralelograma; a svaki kružni segment je manji od paralelograma. Prema tome je svaki od trouglova EKZ, ZLH, HMQ, QNE veći od polovine odgovarajućeg kružnog segmenta. Ako sad prepolovimo kružne lukove, koji nastaju posle prethodne podele, spojimo nove deone tačke dužima i taj postupak produžimo neprekidno, dobićemo kružne segmente čiji je zbir manji od razlike kruga i manje površine S. Zaista, prema prvoj teoremi desete knjige [X.1], ako imamo dve nejednake veličine, iste prirode, pa od veće oduzmemo veličinu veću od njene polovine, od ostatka oduzmemo ponovo veličinu veću od polovine tog ostatka i taj postupak produžimo neprekidno, ostaće neka veličina koja je manja od manje od polaznih veličina. Neka tako bude i neka zbir konstruisanih kružnih segmenata EK, KZ, ZL, LH, HM, MQ, QN, NE kruga EZHQ bude manji od razlike kruga EZHQ i površine S. Tada je ostatak, mnogougao EKZLHMQN, veći od površine S. Upišimo i u krug ABGD mnogougao AXBOGpDP, sličan mnogouglu EKZLHMQN. Tada je kvadrat na BD prema kvadratu na ZQ kao mnogougao AXBOGpDP prema mnogouglu EKZLHMQN [XII.1]. Ali kvadrat na BD prema kvadratu na ZQ odnosi se kao krug ABGD prema površini S. Prema tome je krug ABGD prema površini S kao mnogougao AXBOGpDP prema mnogouglu EKZLHMQN [V.11]. Prema tome, posle promene reda, krug se odnosi prema u nj upisanom mnogouglu kao površina S prema mnogouglu EKZLHMQN [V.16]. Ali krug je veći od mnogougla upisanog u nj, pa prema tome je i površina S veća od mnogougla EKZLHMQN. No ona je i manja. A to je nemoguće. Prema tome nije kvadrat na BD prema kvadratu na ZQ kao krug ABGD prema površini manjoj od kruga EZHQ. Slično se dokazuje da i kvadrat na ZQ prema kvadratu na BD nije kao krug EZHQ prema površini manjoj od kruga ABGD.
Tvrdim, takođe, da ni kvadrat na BD prema kvadratu ZQ neće biti kao krug ABGD prema površini koja je veća od kruga EZHQ.
Zaista, ako je to moguće, neka bude prema većoj površini T. Znači, posle promene reda kvadrat na ZQ je prema kvadratu na DB kao površina T prema krugu ABGD. Ali površina T se odnosi prema krugu ABGD kao krug EZHQ prema površini manjoj od kruga ABGD. Na ovaj način kvadrat na ZQ je prema kvadratu na BD kao krug EZHQ prema površini manjoj od kruga ABGD [V.11]. A dokazano je da je to nemoguće. Prema tome kvadrat na BD prema kvadratu na ZQ ne odnosi se kao krug ABGD prema površini većoj od kruga EZHQ. A dokazali smo da nije ni kao taj krug prema manjoj površini. Prema tome je kvadrat na BD prema kvadratu na ZQ kao krug ABGD prema krugu EZHQ.
Na ovaj način, krugovi se odnose jedan prema drugom kao kvadrati na prečnicima. A to je trebalo dokazati.